在日常生活和工作当中，我们会用一些数据来描述事实，那你有被数据所欺骗吗？本文作者从样本、口径、统计、结构和对比这五个角度分析了数据欺骗我们的小细节，感兴趣的童鞋一起来看看吧。

在日常的工作中，作为数据部门，我们常常说：数据就是领导力。

很多时候，如果工作中发生了冲突，站在A的角度有A的道理，站在B的角度，有B的道理，一上来讲道理是很难达成一致意见的。但是，讲数据是有可能解决分歧的，因为讲数据就是讲事实，事实只可能是一个。

然而，工作和生活中，我们常常发现，就算数据完全真实，我们依然有可能被欺骗，今天就分享一些基本方法，避免被真实的数据欺骗。

一、样本谎言

样本谎言指的是，我们面对的客观对象庞大而复杂，在时间、成本、能力等因素的限制下，没办法做到全量测量，只能对抽取的样本进行测量。抽样的问题在于，如何确保样本能够代表整体。存在极端小样本或者无样本的例子：

• 小样本：中国男足在世界杯漫长历史上仅仅输了三场。
• 无样本：中国男足在02年世界杯后，再也没有输过一场世界杯比赛。

当然，这是段子，有些人说，我把样本的量尽可能多，不就可以避免这个问题。

其实不是的，耳熟能详是1936年美国大选，《文学文摘》杂志调查了240万选民，而盖洛普只调查了5000人，结果盖洛普预测成功。最大的区别在于，盖洛普是按照全部选民的人口结构，同比例进行抽样，样本虽小，但足够典型。

在现实生活中，还有一种场景，是人为地选择性地扩大或者挑选样本，造成对信息接收方的误导。

举个例子，我参加软考，没通过，然后就跟周围人说，软考太难了，通过率甚至不到10%。这的确是个真实的数据。

但我没说的是，软考的弃考率非常高，只有不到30%的考生参加了考试，如果以参加考试考生作为基数，通过率就超过40%，并没有我所说的那么难。

面对一个统计数据，要有意识地确认这个数据究竟是整体，还是样本？样本在整体中的占比是多少、如何进行抽样的？对于想要表达的观点，样本是否有意义。

二、口径谎言

口径谎言，每一个指标都有其统计逻辑，在不知道背后逻辑的情况下，你以为你看到的数据就真的是你想的那样吗？就以现在新冠疫情为例，究竟新冠死亡人数，是die of 还是die with，两者的差距非常大。

在信用卡行业，在比较用户规模的时候，到底是发卡量、还是新增账户还是流通账户，背后的数据就千差万别。即便是相同的指标：新增账户，背后的口径也有非常多细微的差别，反映到数据上，就可能谬以千里。

在不了解具体口径的情况下，盲目根据数据进行判断，就容易掉入数据陷阱。

还有一种情况，就是通过时间轴看趋势的时候，口径虽然没变，但是忽略了重要的变化因素，影响对数据趋势的判断。

举个例子，在分析不良率的时候，直接看数据，会发现指标持续降低，大家看了都很兴奋。

但是，如果你知道不良率=不良余额/贷款余额，你就会思考，不良率的降低，究竟是因为不良余额控制住了，还是贷款余额，把盘子做大了导致的？

如果是后者，那么，风险只是暂时掩盖了而已，不良率数字上的降低是存在欺骗性质的。

面对一个统计指标，需要注意的是，你得了解其中计算逻辑，以及哪些因素的变化可能影响数据的走势。

在使用指标的过程中，要有意识地确认：这个指标可以横向对比吗？可以纵向回溯吗？

三、统计谎言

平均数谎言常见于各类不专业的媒体，比如媒体会经常制造出类似“腾讯员工平均月薪7万”的新闻，很多腾讯员工直呼被平均，现在都成了段子。其实，类似的问题还有很多，比如李克强总理说，我们人均年可支配收入是3万元人民币，但是有6亿中低收入及以下人群，他们平均每个月的收入也就1000元左右。

在分布非常不均匀的时候，用平均数试图描述每个人状况就不合适了，中位数或者众数更能体现真实的情况。另外，还有一种百分比谎言，比如某个专业的研究生，百分百进入大厂，大家惊呼太厉害了，但事实上，可能这个专业同一届毕业研究生可能不到5人。

平均数容易掩盖差距，百分比会掩盖规模，看到统计数据，要学会还原原始值、要学会看分布，多想想背后有哪些特殊情景有可能会扭曲事实。

四、结构谎言

刚毕业的时候我在房地产公司写市场报告，每周我都需要统计当周新房成交单价，进行环比同比，判断房价的走势。有一次，我发现当周的房价出现大幅下降，与当时市场行情相反，我感觉数据有问题。

经过仔细比较，我发现数据是真实的，造成房价波动的原因是当时郊区有个楼盘当天成交了大量房源，影响了成交新房的结构，导致全市的房价被拉低了。进一步可以发现神奇的现象，郊区的大盘和全市其他楼盘的房价都是上涨，但是整体成交的单价却是在下降。

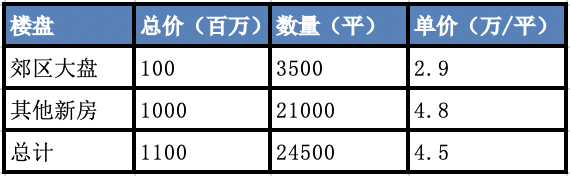
第一周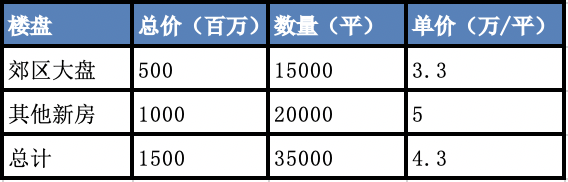

第二周

看表格就可以发现，郊区大盘的每平米单价从2.9万上升到3.3万，其他新房的单价从4.8万上升到5万，整体却从4.5万下滑到了4.3万。这就是著名的辛普森悖论，总体结论和部分结论恰好相反。这提醒我们，要警惕总体结论，要通过科学合理的分组查看具体细致的数据

五、对照谎言

数据是要有比较才能看到问题的。但是，有时候我们一些不恰当的对比，反而会影响我们的判断。典型的例子，比如美国和西班牙交战期间，美国海军的死亡率低于同期纽约市民的死亡率，从而论证士兵更安全。

但事实上，用体格健壮的年轻人的死亡率和包含病人、老人、婴儿的居民死亡率对比，本身就不合理。在做数据分析工作的时候，无视行业周期性波动就会犯这类问题，拿3月份的业绩和春节的业绩进行对比就不合适，用有双十一的业绩和其他月份比也不合理。

当然，这些只是非常明显的例子，还有很多每个企业细微的差异，比如在做竞品报告的时候，选取对本公司最有利的时间节点、城市区域、价格区间等等，会让人产生误导。

除此之外，我们在可视化的时候，其实也会有类似的问题，尤其是Y坐标轴刻度，很容易影响判断。

以下两个图其实数据完全相同，但是Y坐标轴不一致，呈现的信息就不一样了。

涉及数据指标之间比对的时候，必须注意是否存在隐含的条件是有利于其中一方的，比对的双方是否真的有比较意义。

六、小结

以上分别从样本、口径、统计、结构和对比五个角度分析了一些常见的数据欺骗我们的细节，如何避免被数据欺骗，除了上面的应对方案外，还有一些基本的方法：

1. 数据从哪里来

凡是不给出确切数据出处的，需要提高警惕，基本不可信。如果有确切出处的，多想想提供数据的是谁，站在怎样的立场，很多时候，提供数据方的立场会决定数据的样本、口径及呈现方式，英文中有一个词“Half-truth”，即给你看的部分是真的，但它只是事实的一部分。

很多时候我们常说要增加信息源，就是为了避免单一信息源导致的认知偏差。信息多了会有冗余，但冗余也可以避免出错。

2. 漏掉了什么

本质上来说，每个数据对于客观分析对象，都只是一个要素，在系统思维中，除了要素，我们更要关注各个要素之间的连接关系。

指标是怎么算出来的，相关的指标有哪些，指标之间的关系是怎样的，是否遗漏了某个重要的因素？

这就是一种公式思维，用数学公式，来表达要素之间的连接关系，进而关联地看问题和数据。

3. 合乎情理吗

人的天性容易被那些超乎寻常的事物所吸引，不管是媒体上的信息还是很多报告，常常也会因为需要亮点而制造一些异乎寻常的数据。

面对数据的时候，可以尝试将数据放在更大的时空来考量。因为更大的时空提供了基本的信息量，也就是常识。

对于关心的领域，要有足够的常识和判断力，判断力到了一定程度，有一些坑，可能在不经意间就已经绕过去了。

4. 保持敬畏之心

我们的知识、智慧所限，我们能试图破解的系统是有复杂度上限的。

面对看起来非常客观的数据，我们能做的就是猜测、验证、迭代，做任何决策的时候，始终要保持谦卑和敬畏之心。